1417. Queen Move
A queen is placed on an m × n chessboard. Determine how many squares are under its attack.
Input. Four positive integers: the size of the chessboard m and n, as well as the coordinates of the queen x and y (1 ≤ x ≤ m ≤ 109, 1 ≤ y ≤ n ≤ 109).
Output. Print the number of squares under the queen’s attack.
|
Sample
input |
Sample
output |
|
8 8 4 5 |
27 |
SOLUTION
mathematics
Algorithm analysis
The queen is a
chess piece that moves (and attacks) horizontally, vertically, and diagonally.
The row where
the queen is placed contains n squares, so the number of squares
available for horizontal movement is n – 1. Similarly, the
column where the queen is located contains m squares, meaning the number
of squares available for vertical movement is m – 1.
Thus, the number
of squares under the queen’s attack horizontally and vertically is n – 1 + m – 1.

Divide the board into four
areas by drawing horizontal and vertical lines through the square where the
queen is located. In each of these areas, count the number of squares under her
attack.
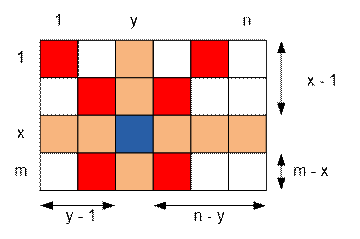
Consider, for example, the
upper-right quadrant. Its length is n
– y squares, and its width is x – 1 squares. Therefore, the number of
squares under the queen’s attack in this area is min(x – 1, n – y).
Similarly:
·
In the upper-left quadrant, there are min(x – 1, y – 1) squares;
·
In the lower-left quadrant, there are min(m – x,
y – 1) squares;
·
In the lower-right quadrant, there are min(m – x,
n – y) squares;
Example
Consider the
example where the board size is 8 × 8 and the queen is located at
position (4, 5).
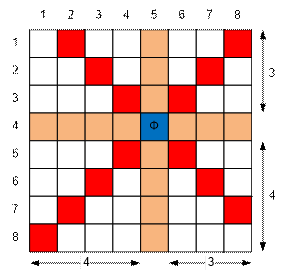
The number of squares
under the queen’s horizontal and vertical attack is n – 1 + m – 1 = 7 + 7 = 14. Now, let’s consider the
four quadrants, in each of which we’ll count the number of squares under its
attack:
·
in the upper left quadrant there are min(4, 3) = 3
squares;
·
in the lower left quadrant there are min(4, 4) = 4
squares;
·
in the lower right quadrant there are min(3, 4) = 3
squares;
·
in the upper right quarter there are min(3, 3) = 3
squares;
Thus, the total number of
squares under the queen’s attack is
14 + 3 + 4 + 3 +
3 = 27
Algorithm implementation
Read the input data.
scanf("%d %d %d
%d", &m, &n, &x, &y);
Store in the variable s the number of squares
under the queen’s attack from horizontal and vertical moves.
s = m - 1 + n - 1; //
horiz & vertical
Then, add the squares that the queen attacks along the
diagonals.
s += min(m - x, n - y); // (x,y) -> (m, n)
s += min(m - x, y - 1); // (x,y) -> (m, 1)
s += min(x - 1, n - y); // (x,y) -> (1, n)
s += min(x - 1, y - 1); // (x,y) -> (1, 1)
Print the answer.
printf("%lld\n",
s);